CONTENTS
备注:
本读书笔记基于侯捷先生的《STL源码剖析》,截图和注释版权均属于原作者所有。
本读书笔记中的源码部分直接拷贝自SGI-STL,部分代码删除了头部的版权注释,但代码版权属于原作者。
小弟初看stl,很多代码都不是太懂,注释可能有很多错误,还请路过的各位大牛多多给予指导。
为了降低学习难度,作者这里换到了SGI-STL-2.91.57的源码来学习,代码下载地址为【 http://jjhou.boolan.com/jjwbooks-tass.htm 】
根据侯捷先生所著《STL源码剖析》可知,STL中的heap本质上是一棵最大完全二叉树。
1 整个树除了最底层的节点外,其余各层都是填满的。最底层如果不满,则从左至右是没有空隙的。
2 每个节点值都大于等于其子节点值。
stl_heap.h:
push_heap:
//插入一个元素到最大完全二叉树中。
//first:最大完全二叉树的根节点的iterator值。
//holeIndex:要插入的完全二叉树的节点的编号,即当前空闲节点编号。
//topindex:要插入的值在二叉树中的最小的节点编号,
//value:要插入的值。
template <class RandomAccessIterator, class Distance, class T>
void __push_heap(RandomAccessIterator first, Distance holeIndex,
Distance topIndex, T value) {
Distance parent = (holeIndex - 1) / 2;//首先根据当前空闲节点编号算出其父节点编号。
while (holeIndex > topIndex && *(first + parent) < value) {
//如果要插入的值>父节点的值,就把父节点和当前节点互换,然后继续循环比较。
*(first + holeIndex) = *(first + parent);
holeIndex = parent;
parent = (holeIndex - 1) / 2;
}
//循环结束之后,将value放入找到的节点里。
*(first + holeIndex) = value;
}
如下图,加入要把80插入当前的二叉树中,那么80首先会找到其父节点50,由于80>50,那么就将50放到之前要插入80的位置,然后把80的插入位置更新为50所在的节点,再次循环比较。找到80当前插入位置的父节点即60,80>60。同样,将60和80的位置互换。再次循环比较,找到80插入位置的父节点90,80<90.无需位置互换。此时80的插入位置已经找到了。就将80插入即可。

//整理成最大完全二叉树。
//这里提供两个iterator,分别指向存储树的数据结构的起始最后位置。
//这里吧数据结构的最后一个节点插入二叉树中。
//这里的意思是该数据结构中除了最后一个元素外其他的元素都符合最大完全二叉树。这里最后一个元素是刚刚插入的,需要整理一下才能让整个数据结构符合最大完全二叉树。
//比如数组【90,70,60,50,50,50,55,40,30,20,10,80】,如上图所示。除了最后一个元素80外,其他的元素都符合最大完全二叉树。
//这里first指向90,last指向80之后的下一个元素。last-1指向80
template <class RandomAccessIterator, class Distance, class T>
inline void __push_heap_aux(RandomAccessIterator first,
RandomAccessIterator last, Distance*, T*) {
__push_heap(first, Distance((last - first) - 1), Distance(0),
T(*(last - 1)));
}
//整理成最大完全二叉树。
template <class RandomAccessIterator>
inline void push_heap(RandomAccessIterator first, RandomAccessIterator last) {
__push_heap_aux(first, last, distance_type(first), value_type(first));
}
//和上面的代码一样,只不过是添加了自定义比较函数
template <class RandomAccessIterator, class Distance, class T, class Compare>
void __push_heap(RandomAccessIterator first, Distance holeIndex,
Distance topIndex, T value, Compare comp) {
Distance parent = (holeIndex - 1) / 2;
while (holeIndex > topIndex && comp(*(first + parent), value)) {
*(first + holeIndex) = *(first + parent);
holeIndex = parent;
parent = (holeIndex - 1) / 2;
}
*(first + holeIndex) = value;
}
//和上面的代码一样,只不过是添加了自定义比较函数
template <class RandomAccessIterator, class Compare, class Distance, class T>
inline void __push_heap_aux(RandomAccessIterator first,
RandomAccessIterator last, Compare comp,
Distance*, T*) {
__push_heap(first, Distance((last - first) - 1), Distance(0),
T(*(last - 1)), comp);
}
//和上面的代码一样,只不过是添加了自定义比较函数
template <class RandomAccessIterator, class Compare>
inline void push_heap(RandomAccessIterator first, RandomAccessIterator last,
Compare comp) {
__push_heap_aux(first, last, comp, distance_type(first), value_type(first));
}
pop_heap:
//从上到下调整二叉树。当二叉树被删掉了某个父节点后,重新从子节点中找到最大值。
//需要调整下才可以恢复成最大完全二叉树。
//first:最大完全二叉树的根节点的iterator值。
//holeIndex:要调整的二叉树的根节点,一般来讲,该根节点不符合二叉树的要求
//len:二叉树调整的最大范围。
template <class RandomAccessIterator, class Distance, class T>
void __adjust_heap(RandomAccessIterator first, Distance holeIndex,
Distance len, T value) {
Distance topIndex = holeIndex;
Distance secondChild = 2 * holeIndex + 2;//首先找到右子节点
while (secondChild < len) {
if (*(first + secondChild) < *(first + (secondChild - 1)))//在两个子节点中找到一个比较大的节点
secondChild--;
*(first + holeIndex) = *(first + secondChild);//然后把父节点和较大子节点互换
holeIndex = secondChild;//然后继续循环比较。
secondChild = 2 * (secondChild + 1);
}
//特殊情况处理,如果比较到最后发现最后的右子节点就是最开始换过的节点,那么就不在比较,直接和左子结点互换。
//因为这里最后面的那个节点会被删掉,所以不用关心。
//个人感觉先和左子节点比较下更好,虽然下面有__push_heap。
if (secondChild == len) {
*(first + holeIndex) = *(first + (secondChild - 1));
holeIndex = secondChild - 1;//这里的holeIndex向前进了一格,因此后面的__push_heap会跳过最后一格。
}
//将调整后的树调用__push_heap,如果是pop_heap,那么基本上没有作用,如果是make_heap,可以将原来的元素重新入树。
__push_heap(first, holeIndex, topIndex, value);
}
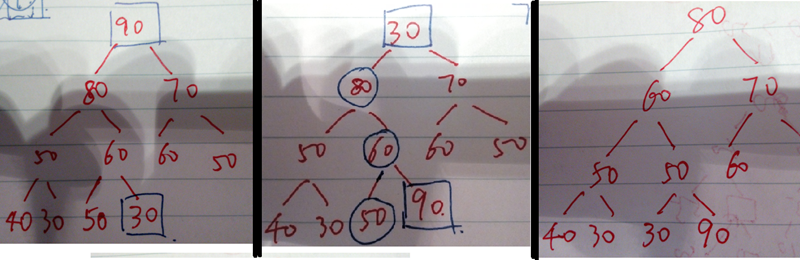
如下图,这里加入我们要删除90,那么我们就把90和最后的一个元素30互换,这样30成了根节点。为了让新的二叉树符合要求,这里就把30和其子节点中的较大值80比较,30<80,互换后继续比较,新的子节点的较大值为60,30<60,继续互换比较后循环,但是这里就进入了特殊情况,30的右子节点就是最后的节点90,这样便不会比较,会退出循环,然后直接和50互换。最后调用push_heap,重新检查一下。
//弹出树顶节点。调用__adjust_heap。
template <class RandomAccessIterator, class T, class Distance>
inline void __pop_heap(RandomAccessIterator first, RandomAccessIterator last,
RandomAccessIterator result, T value, Distance*) {
*result = *first; //首先获取到根节点值。
__adjust_heap(first, Distance(0), Distance(last - first), value);
}
template <class RandomAccessIterator, class T>
inline void __pop_heap_aux(RandomAccessIterator first,
RandomAccessIterator last, T*) {
//注意这里的last均减1传入,这样最后的那个元素在__push_heap时便会被略掉。
__pop_heap(first, last - 1, last - 1, T(*(last - 1)), distance_type(first));
}
template <class RandomAccessIterator>
inline void pop_heap(RandomAccessIterator first, RandomAccessIterator last) {
__pop_heap_aux(first, last, value_type(first));
}
//和上面的代码一样,只不过是添加了自定义比较函数
template <class RandomAccessIterator, class Distance, class T, class Compare>
void __adjust_heap(RandomAccessIterator first, Distance holeIndex,
Distance len, T value, Compare comp) {
Distance topIndex = holeIndex;
Distance secondChild = 2 * holeIndex + 2;
while (secondChild < len) {
if (comp(*(first + secondChild), *(first + (secondChild - 1))))
secondChild--;
*(first + holeIndex) = *(first + secondChild);
holeIndex = secondChild;
secondChild = 2 * (secondChild + 1);
}
if (secondChild == len) {
*(first + holeIndex) = *(first + (secondChild - 1));
holeIndex = secondChild - 1;
}
__push_heap(first, holeIndex, topIndex, value, comp);
}
template <class RandomAccessIterator, class T, class Compare, class Distance>
inline void __pop_heap(RandomAccessIterator first, RandomAccessIterator last,
RandomAccessIterator result, T value, Compare comp,
Distance*) {
*result = *first;
__adjust_heap(first, Distance(0), Distance(last - first), value, comp);
}
template <class RandomAccessIterator, class T, class Compare>
inline void __pop_heap_aux(RandomAccessIterator first,
RandomAccessIterator last, T*, Compare comp) {
__pop_heap(first, last - 1, last - 1, T(*(last - 1)), comp,
distance_type(first));
}
template <class RandomAccessIterator, class Compare>
inline void pop_heap(RandomAccessIterator first, RandomAccessIterator last,
Compare comp) {
__pop_heap_aux(first, last, value_type(first), comp);
}
make_heap:
//构造一个最大完全二叉树
template <class RandomAccessIterator, class T, class Distance>
void __make_heap(RandomAccessIterator first, RandomAccessIterator last, T*,
Distance*) {
if (last - first < 2) return;
Distance len = last - first;
Distance parent = (len - 2)/2;//最下边,最右边的最小子树的根节点。
while (true) {
//注意这里第4个参数是T(*(first + parent)),即将弹出的元素再插入。这样树的元素保持不变,
//但是会变为最大二叉树。
__adjust_heap(first, parent, len, T(*(first + parent)));
if (parent == 0) return;
parent--;
}
}
//构造一个最大完全二叉树
template <class RandomAccessIterator>
inline void make_heap(RandomAccessIterator first, RandomAccessIterator last) {
__make_heap(first, last, value_type(first), distance_type(first));
}
template <class RandomAccessIterator, class Compare, class T, class Distance>
void __make_heap(RandomAccessIterator first, RandomAccessIterator last,
Compare comp, T*, Distance*) {
if (last - first < 2) return;
Distance len = last - first;
Distance parent = (len - 2)/2;
while (true) {
__adjust_heap(first, parent, len, T(*(first + parent)), comp);
if (parent == 0) return;
parent--;
}
}
//构造一个最大完全二叉树,使用自定义比较
template <class RandomAccessIterator, class Compare>
inline void make_heap(RandomAccessIterator first, RandomAccessIterator last,
Compare comp) {
__make_heap(first, last, comp, value_type(first), distance_type(first));
}
如下图所示,parent的值为最下,最右子树的根节点,通过不断递减,便会由右至左,有下至上不断的对子树进行排序,当parent为0时,说明已经排序到了根节点,树就完成了。

sort_heap:
//通过不停的弹出最大元素,生成一个递增序列。
template <class RandomAccessIterator>
void sort_heap(RandomAccessIterator first, RandomAccessIterator last) {
while (last - first > 1) pop_heap(first, last--);
}
template <class RandomAccessIterator, class Compare>
void sort_heap(RandomAccessIterator first, RandomAccessIterator last,
Compare comp) {
while (last - first > 1) pop_heap(first, last--, comp);
}
发表评论