【转】Levenshtein Distance （LD算法） 编辑距离算法原理

本文转自【Levenshtein Distance （LD算法） 编辑距离算法原理_Steve_Stone的博客-CSDN博客_编辑距离算法原理】，有删改。

LD算法介绍

莱文斯坦距离，又称Levenshtein距离，是编辑距离的一种。指两个字串之间，由一个转成另一个所需的最少编辑操作次数。允许的编辑操作包括：将一个字符替换成另一个字符，插入一个字符，删除一个字符。

LD算法目的：计算出两字符序列的编辑距离，同时也能求出两序列的匹配序列

假设比对的俩序列为：

则两序列的长度分别为len(A)=n Len(B)=m
LD(A,B)：字符串A和字符串B的编辑距离，即将字符串A转换为字符串B所用的最少字符操作数。
LD(A,B)=0表示两个字符串完全一样。
LD(i,j)=LD(a1a2……ai,b1b2……bj)，其中0≤i≤n，0≤j≤m

算法步骤：

1.初始化算法分数矩阵H，使行i表示字符ai，列j表示字符bj；

2.计算矩阵中每一项的LD(i, j)：
若ai = bj，则LD(i, j) = LD(i-1, j-1) 取左上角的值
若ai ≠ bj，则LD(i, j) = Min( LD(i-1, j-1), LD(i-1, j), LD(i, j-1) ) +1

3.回溯，从矩阵右下角开始：
若ai=bj，则回溯到左上角单元格；
若ai≠bj，回溯到左上角、上边、左边中值最小的单元格，若有相同最小值的单元格，优先级按照左上角、上边、左边的顺序。

4.根据回溯路径，写出匹配字符串：
若回溯到左上角单元格，将ai添加到匹配字串A‘，将bj添加到匹配字串B’；
若回溯到上边单元格，将ai添加到匹配字串A’，将_添加到匹配字串B’；
若回溯到左边单元格，将_添加到匹配字串A’，将bj添加到匹配字串B’。

5.矩阵右下角的值即为俩序列的编辑距离，回溯结果为全部匹配序列。

示例：

A=GGATCGA，B=GAATTCAGTTA

1.评分矩阵：

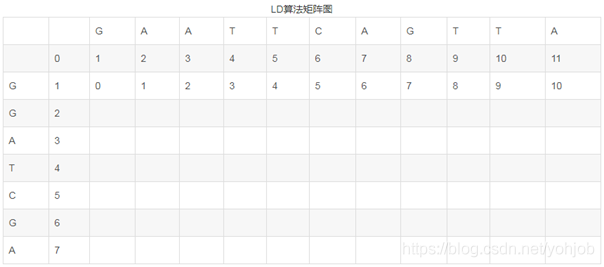
2.回溯：

3.结果：
LD(A,B) = 5;

可见LD算法的流程和needleman wunsch算法是很类似的，区别在于LD算法使用的是最小值，NW算法使用的是最大值。