《编程之美》读书笔记：烙饼排序问题

最近在学习《 编程之美 》这本书，书中提到了很多很经典的算法问题和实现，学起来真是耗费脑细胞啊。书中的算法实现使用C编写的，这里作者自己写了一部分java的实现，如果有错误，还请各位读者批评指正。截图版权属于原作者。

github：

【 https://github.com/cstriker1407/think_in_java 】

第1.3节：烙饼排序问题：

解法1，每次翻转最大的拿张：

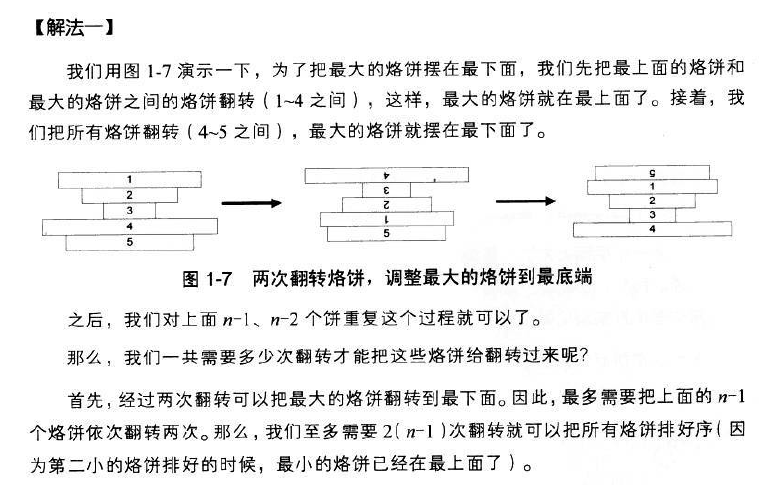
代码如下：

private static final int[] UnSortArr = {1,5,3,4};//,6,2,9,8,7};
//获取最大值
public static int getMaxSortNum()
{
	LinkedList<Integer> middleList = new LinkedList<Integer>();
	for (int item : UnSortArr)
	{
		middleList.add(item);
	}
	System.out.println("未排序：" + middleList.toString());
	int reverseTime = 0;
	int totalNum = middleList.size();
	int numNoSort = totalNum;
	while (numNoSort > 0)
	{
		/* sublist：
		 * 返回列表中指定的 fromIndex（包括 ）和 toIndex（不包括）之间的部分视图。（如果 fromIndex 和 toIndex 相等，则返回的列表为空）。
		 * 返回的列表由此列表支持，因此返回列表中的非结构性更改将反映在此列表中，反之亦然。返回的列表支持此列表支持的所有可选列表操作。
		 */
		//从没有排序的list里面找到最大的一个数，以及它的ID
		int maxNum = Collections.max( middleList.subList(0, numNoSort));
		int maxNumIdx = middleList.indexOf(maxNum);
		
		//翻转最大数到第一个数之间的所有的数据
		Collections.reverse( middleList.subList(0, maxNumIdx + 1) );
		System.out.println("找到最大数["+ maxNum +"]并翻转：" + middleList.toString());
		reverseTime++;
		
		//翻转第一个数和没有排序的最后一个数间的所有数据
		Collections.reverse( middleList.subList(0, numNoSort) );
		System.out.println("将最大数翻到底部：" + middleList.toString());
		reverseTime++;
		
		//没有排序的数据个数--
		numNoSort--;
	}
	System.out.println("总数:"+ totalNum +" 翻转次数为：" + reverseTime);
	return reverseTime;
}

 Java的关于list的工具类比较多，也比较好用，实现起来相对容易一点。

通过枚举方法来获取最小的数目：

首先备份下用到的工具函数：

//判断是否排序OK
private static boolean isListSorted(LinkedList<Integer> middleList)
{
	for (int i = 1; i < middleList.size(); i++)
	{
		if(middleList.get(i-1) >= middleList.get(i))
		{
			return false;
		}
	}
	return true;
}

 使用递归的方法，在上一次翻转的基础上进行二次翻转：

/*
 *在当前已经进行部分翻转的list上面进行下一次的翻转，并且对翻转的序号x【0，x】进行遍历
 *times表示当前已经翻转的次数
 */
private static void internalSort(LinkedList<Integer> middleList, int times)
{
	//已经排序OK，不用再测试了。
	if (isListSorted(middleList))
	{	//记录最小值
		minSortNum = times < minSortNum ? times : minSortNum;
		return;
	}
	
	/*
	 *加速判断，根据getMaxSortNum函数的测试，可以发现最大值为数据list长度的2倍，因此当
	 *当前的翻转数目 + 估计剩余的最小翻转数 > middleList.size() * 2，可以认为这次翻转已经没有意义了
	 */
	if (times + getMinSortNum() > maxSortNum)
	{
		return;
	}
	
	/*
	 * 既然不知道如何翻转数目最小，那我们就遍历，在当前已经部分翻转之后的list上，进行二次翻转，每次翻转的个数【i】进行遍历。
	 * 翻转完成之后将数据还原，方便下次翻转。
	 */
	for (int i = 0; i < middleList.size(); i++)
	{
		Collections.reverse( middleList.subList(0, i + 1) );
		internalSort(middleList, times + 1);
		Collections.reverse( middleList.subList(0, i + 1) );
	}
}

 为了加速计算，减少不必要的递归，我们计算出翻转次数的上下限。（下限是估计出来的）

//获取最小估计值，不准确。
public static int getMinSortNum()
{
	int num = 0;
	for (int i = 1; i < UnSortArr.length; i++)
	{
		//如果相邻的两个饼的大小也相邻，那么就可以认为这两个饼是一个整体
		if (UnSortArr[i] - UnSortArr[i-1] == 1 || UnSortArr[i] - UnSortArr[i-1] == -1)
		{
		}else
		{
			num++;
		}
	}
	return num;
}

 最后是入口测试函数：

public class SortTest
{
	private static final int[] UnSortArr = {1,5,3,4};//,6,2,9,8,7};
	
	//最小的翻转次数
	private static int minSortNum = Integer.MAX_VALUE;
	//最大的翻转次数
	private static int maxSortNum = -1;
	
	//在当前已经进行部分翻转的list上面进行下一次的翻转
	public static void testSort(  )
	{
		maxSortNum = getMaxSortNum();
		
		LinkedList<Integer> middleList = new LinkedList<Integer>();
		for (int item : UnSortArr)
		{
			middleList.add(item);
		}
		System.out.println("未排序：" + middleList.toString());
		internalSort(middleList, 0);
		
		System.out.println("最小数目：" + minSortNum);
		System.out.println("最大数目：" + maxSortNum);
	}
	
	//判断是否排序OK
	private static boolean isListSorted(LinkedList<Integer> middleList)
	{
	。。。。。。
	}

	/*
	 *在当前已经进行部分翻转的list上面进行下一次的翻转，并且对翻转的序号x【0，x】进行遍历
	 *times表示当前已经翻转的次数
	 */
	private static void internalSort(LinkedList<Integer> middleList, int times)
	{
	。。。。。。
	}
	
	
	//获取最小估计值，不准确。
	public static int getMinSortNum()
	{
	。。。。。。
	}
	
	//获取最大值
	public static int getMaxSortNum()
	{
	。。。。。。
	}
}